Use of STACK in Honours Complex Variables

Context

Complex analysis is a classical branch of pure mathematics, and one of the high points of human intellectual achievement. The University of Edinburgh complex analysis course, Honours Complex Variables, is typically taken by around 250 students annually, mostly in Year 3 of Mathematics BSc/MMath degrees. The course covers the following topics:

• holomorphic functions, the Cauchy-Riemann equations, and multivalued functions;
• conformal maps, the extended complex plane, Riemann sphere, and Möbius transformations;
• Cauchy's Integral Theorem, and the (Generalized) Cauchy Integral Theorem;
• Liouville's Theorem and the Maximum Modulus Principle;
• Taylor and Laurent Series;
• zeros, singularities, residues, and the Cauchy Residue Theorem; and
• evaluation of real integrals using contour integrals.

The course content is based on an established set of course notes (around 80 pages) written by Dr Richard Gratwick, the current course organiser. The notes contain the background theory, proofs, examples and some exercises for the students to practise. Students were expected to work on them while they were studying each lecture's content. In addition to the exercises there are also tasks used in face to face workshops.

Execution

Traditionally, the course would have had three 50-minute whole-class lectures and one 50-minute workshop each week. In the academic year 2021-22, the course was redesigned in response to constraints imposed by pandemic restrictions.
The course ran with two 50-minute synchronous digital lectures each week, in which the lecturer used a form of flipped classroom with polling in Zoom, and one 50-minute in-person workshop. The notes were converted from a static PDF to a collection of quizzes in the STACK service.
Each week the students had 3-4 STACK quizzes, and taking into consideration the design of the quizzes, we estimate that the students would need 1-2 hours to work through each of them. So, each week we expect the students to spend 10-12 hours on the course in total (contact hours, quizzes, workshop, assignments). The STACK quizzes were used for practise and they didn't contribute towards the final mark of the course.

This redesign was influenced by the previous work at the University of Edinburgh developing two fully online courses Fundamentals of Algebra and Calculus (FAC) and Introductory Mathematics and its Applications (IMA) [1].
The resources for Honours Complex Variables were created by Richard Gratwick, Steven O’Hagan, the postgraduate intern Ivona Gjeroska and the undergraduate interns Maddy Baron and Xie Jin Ng, in collaboration with Giampaolo D’Alessandro (University of Southampton). The redesign aimed to be future-proof in the sense that materials created should be suitable for reuse in subsequent years, with iterated improvements, even when a return to fully on-campus teaching is possible.

Results

A typical pattern of content from the resource is shown in following figure. We see a definition followed a short discussion and video clip of a worked example by the lecturer. Then we have a STACK question inviting the student to check their own understanding of the material. In addition, each unit of work started with a video of the lecturer giving a high-level overview and motivation of the material to come.

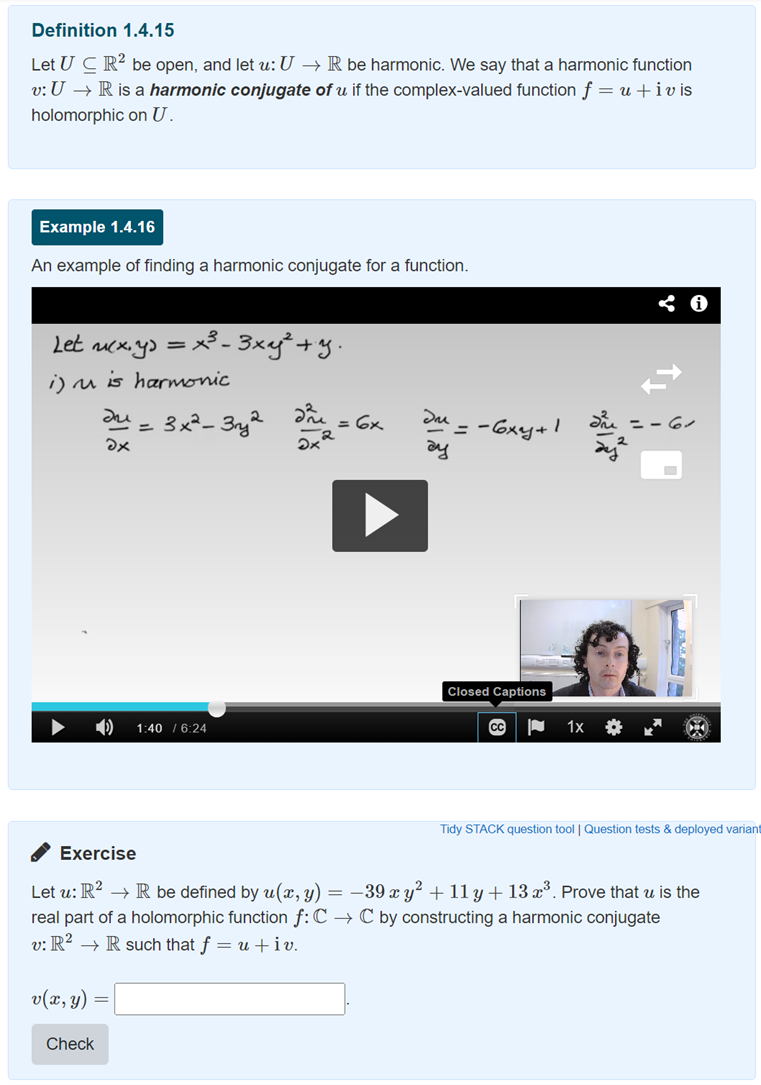
Here are some examples of notable questions created for this course.

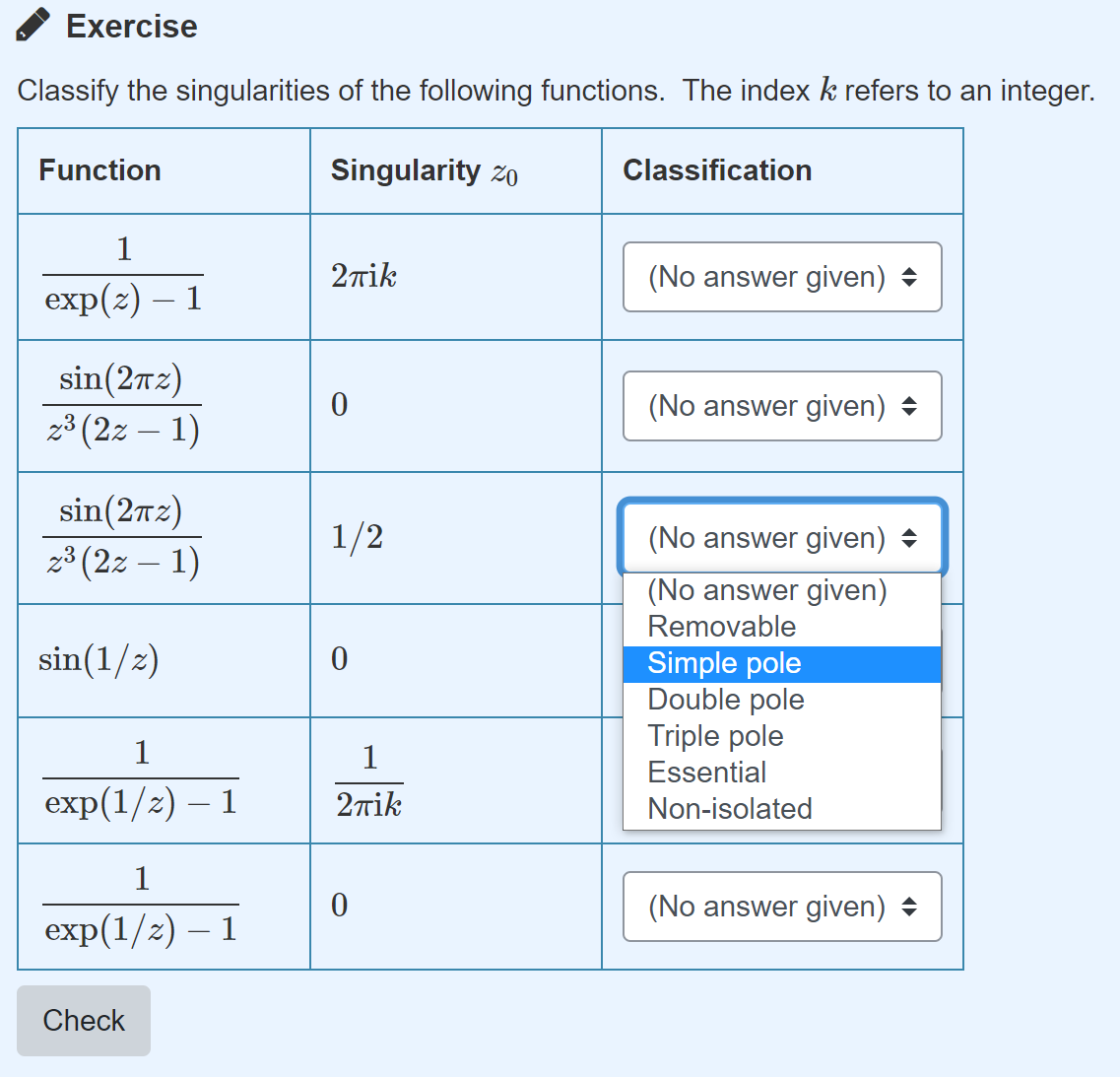
In the future, such sessions could easily translate to on-campus activities using peer instruction, which had been an established practice in the School before the pandemic.

Students' engagement

Student feedback on the course was overwhelmingly positive, with one student responding to the end-of-course survey as follows.

“Genuinely this course has been the perfect mix of activities for my learning, I’d go as far say to the best organised course I’ve taken in SoM, certainly this year anyway. The notes being delivered in stack are great and much more engaging than a pdf (the supplementary pdf is much more easy to navigate for finding Theorems etc. however), which actually makes me do all the reading before lectures so I gain so much more from them. Stack is good in part because of the instant feedback on most exercises which are immediately relevant to what you’re learning, but also because it breaks the material up well. Stack being the main resource works in perfectly with the 2 lectures delivered a week and the tutorial. SoM should considering delivering all courses in this fashion.”

The course organiser, Richard Gratwick, said:

“I believe the redesign of this course has been highly successful, and I like to consider the mode of delivery as a prototype for courses of the future. The motivation was to reflect on the innovations forced upon on us during the pandemic and attempt to implement in a considered way those that proved valuable. Recording short videos of examples and calculations allowed me to present these items “dynamically”, rather than as plain text, but freed up time in synchronous lectures for me to engage with more conceptual high-level discussion of the material. The Stack questions for self-assessment were largely based on exercises included in the previous version of the written notes, but students engaged with them much more regularly when they were presented in the online workbooks – my impression was that in previous years these written exercises were largely ignored.

Challenges

Redesigning a 3rd Year course, so that it contains a substantial amount of online components, was a challenging procedure.

• Authoring questions from scratch: a lot of the STACK questions had to be created completely from scratch because we didn't have any similar questions used in other courses.
• Deciding how to deliver each part of the course: it required careful though to decide which of the questions included in the lecture notes to have as exercise for students to solve or as a written example or as a worked example in a video.
• Some parts of the course can not be assessed automatically. After some consideration the lecturer decided to move some of the easy workshop questions into STACK and used the workshop time to address more complicated questions.

Conclusions

Online assessment it typically used for larger classes in early years of a university mathematics degree, such as calculus or linear algebra. These courses have a strong methods component. As the subject progresses, especially where there is a focus on mathematical proof, it is harder to write online questions which assess the key concepts. As a community we are gaining experience in using quizzes to structure learning materials (rather then traditional lectures), and in supporting more advanced courses. For example the University of Warwick used self-assessed online quizzes in real analysis that would supplement traditional problem sheets. In this course we have demonstrated that STACK can be successfully applied to a higher-level course to promote students' engagement with the content of the course. This is not as straightforward as in calculus and linear algebra, but nevertheless with careful design of materials it is possible to support students online with STACK in advanced courses such as complex analysis.