Question Answering in STACK Applying String Similarity

Hochschule Esslingen

Achim. Eichhorn and Andreas Helfrich-Schkarbanenko

Abstract

We present a method to evaluate fill-in-the-blank student answers in STACK using a string metric. To increase the quality of the evaluation, we use two lists: allowlist and denylist instead of a single teacher's answer. We also show a STACK question equipped with a string metric, by evaluating its use in mathematics courses.

String similarity

The fill-in-the-blank questions are important from a didactic point of view. But they can be hardly implemented, since typing and spelling errors, synonyms and geuine alternatives have to be taken into account when evaluating the students' answers.

To automatically mark fill-in-the-blank questions we used one of the string metrics for measuring the distance between two strings: the Damerau-Levenshtein distance [1, 2], which plays an important role in natural language processing. Informally, this distance is the minimum number of single-character edits (insertion, deletion, substitution, transition) required to change one string sequence into the other. Note that this distance is a metric in mathematical sense, in particular it satisfies the triangle inequality. This enables a suitable string evaluation.

To increase the quality of the assessment, we extended the basic metric function by the adding the components: allowlist and denylist. To have a relative measure of the difference between two strings, we convert the distance to similarity. Applying the similarity on allowlist and denylist we define an acceptance domain for the students' answers. Here we need an empirically determined threshold parameter.

Note that the presented method is, strictly speaking, not only based on the strings, but also on semantics, because by introducing the denylist and allowlist respectively, a (trivial) semantic graph consisting of two clusters is set up. For the sake of simplicity, the evaluation of a student's answer does not take place by means of a semantic distance, but using the string distance to the respective cluster as a whole (single linkage, minimum distance, nearest neighbour, see for example [3]).

The Mathematics

If the Damerau-Levenshtein distance between strings $a$ and $b$ is $\mathbf{d}(a,b) \in [0,\max\{ |a|, |b| \}]$ then the similarity is defined as $$\mathbf{s}(a,b) := 1- \frac{\mathbf{d}(a,b)}{\max\{ |a|, |b| \}}$$ Given lists $$\mbox{allowlist} = \{ TA_1, TA_1, TA_1, \cdots \}$$ $$\mbox{denylist} = \{ WA_1, WA_1, WA_1, \cdots \}$$ then $$\mathbf{s}(a,\mbox{list}) := \max_{k=1,\cdots, K} \mathbf{s}(a,b_k)$$ We then have an acceptance domain in which $$\left( \mathbf{s}(a,\mbox{allowlist}) > \mathbf{s}(a,\mbox{denylist}) \right) \wedge \left( \mathbf{s}(a,\mbox{allowlist}) > \theta \right)$$ for some chosen similarity tollerance $\theta$.

Here are some examples using the strings "Circle", "Triangle" and "Rectangle", together with their Damerau-Levenshtein distance / similarity.

Experiments

We asked students for a suitable solution method by using a fill-in-the-blank question when given a differential equation, see subtask a). This task was used in the winter semester 2021/22 as part of a mini-test for the lecture Mathematics 2. It was completed by 53 students and all student answers were scored error-free.

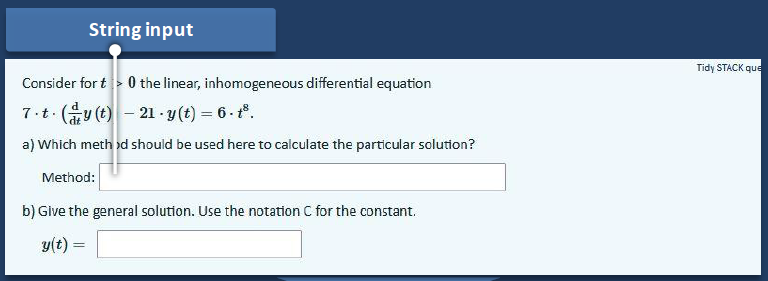
We implemented a string metric directly in the computer algebra system MAXIMA and placed the corresponding function in the Question Variables field of the STACK question concerned. The corresponding XML file can be downloaded from this link (June 2022).

In the bottom figure we see 18 different student answers (in German) which are positioned in a coordinate system according to both similarities and are classified without errors. The radii of the disks represent the number of equal student answers. In total, this task was processed 263 times. The acceptance domain for correct answers is white-marked.

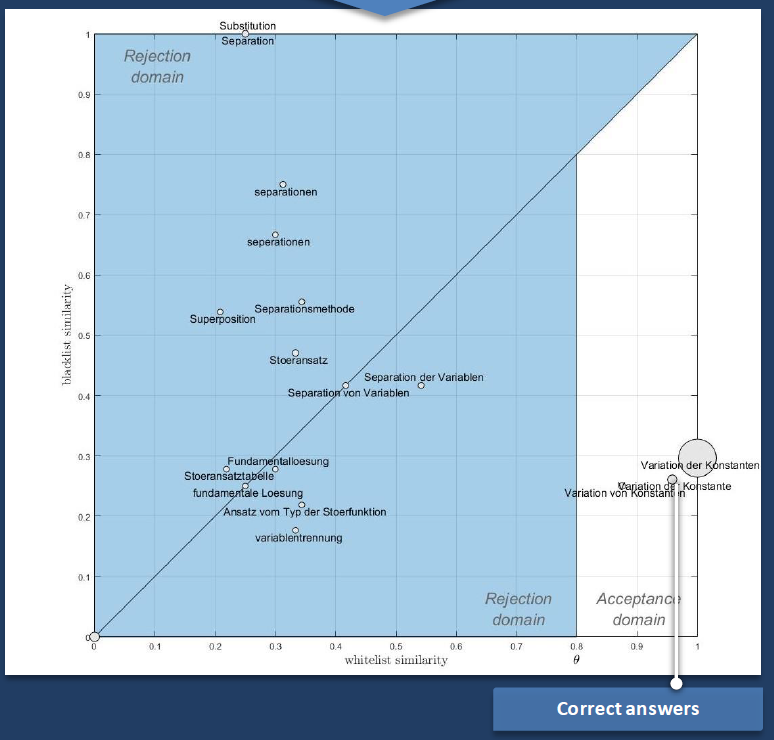
Note that for this STACK question and the given allowlist resp. denylist, only the consideration of the allowlist similarity would be sufficient for the evaluation. However, there are situations where the denylist is necessary.

The authors would like to thank Stiftung Innovation in der Hochschullehre for supporting the project "Digitalisierung Didaktisch Denken".

Implemention notes

This feature has been added to STACK 4.0 in 2022 as an answer test.

References

[1] F. J. Damerau: A technique for computer detection and correction of spelling errors, Communications of the ACM, 7 (3): 171-176 (1964)

[2] Vladimir I. Levenshtein: Binary codes capable of correcting deletions, insertions, and reversals, Soviet Physics Doklady, 10 (8): 707-710, (1966)

[3] A. Eichhorn, A. Helfrich-Schkarbanenko: Question Answering in STACK Applying String Similarity. Private communication, (2022)