optes: Optimising Self-study With STACK
DHBW Mannheim
Miriam Weigel, Katja Derr, Reinhold Hübl
Abstract
The optes project uses STACK in their pre-course, designed to help students improve their self-studying skills for their first year at university. The tests were developed and maintained at DHBW Mannheim. Here, students take a diagnostic test, and based on their results are given access to various learning modules, comprising text, graphs, animations, examples and exercises. An analysis of data gathered from the first evaluation phase of the project shows that the pre-course is effective at bridging gaps in school knowledge: at-risk students who end up scoring highly in the pre-course show improved performance in their first year mathematics courses.
Introduction
Students entering higher education are a diverse group and many students have considerable gaps in school knowledge, putting additional pressure on their first year at university. This particularly applies to mathematics, as basic skills in this subject are considered a prerequisite to successfully complete a course in STEM subjects. As a consequence, many universities provide preparatory courses in mathematics, either face-to-face, web-based, or in blended learning scenarios.
The joint research project optes, funded by the German Federal Ministry of Education and Research (BMBF), develops and evaluates learning materials and tools that help students “refresh” their basic knowledge in mathematics and support the development of learning strategies. optes stands for “Optimierung der Selbststudiumsphase”, which translates to "optimisation of the self-study phase".
Over the course of eight years, optes developed a comprehensive web-based pre-course consisting of diagnostic tests, learning modules and concepts for web-based student support, and tested it at the participating universities. The partner universities include Baden-Wuerttemberg Cooperative State University (DHBW) Karlsruhe, DHBW Mannheim, DHBW Mosbach, University of Applied Sciences and Arts Ostwestfalen-Lippe, Universität Hamburg; Cooperating universities: Julius-Maximilians-Universität Würzburg, University of Education Heidelberg.
Why Use STACK?
The project put a strong focus on the development of self-tests that enable learners to apply their knowledge and provide them with meaningful feedback. This required a sophisticated CAA system, especially one that allowed students to enter an algebraic input. Since optes results are published under Creative Commons or General Public licenses, it was also important that the system was open source. To find the most suitable CAA system, the researchers analysed and compared many existing mathematical tools and in 2013, STACK was chosen. One of the reasons for choosing STACK, is that STACK uses the Learning Management System (LMS) Moodle and the Computer Algebra System (CAS) Maxima, both of which are supported by large communities. This gave the researchers confidence that STACK would also be used and developed further. Additionally, STACK is flexible enough to allow researchers to design very different types of mathematical problems. The only barrier was that STACK was not available for the LMS ILIAS at the time, a system widely used in Germany. However a crowd funding initiative was successful in gathering enough funds to implement STACK into ILIAS.
Execution
The partner university DHBW Mannheim was responsible for the development of tests and self-assessments. Here, a very basic version of the pre-course was implemented in 2013, and based on repeated evaluations, the different tests and learning modules were successively built and improved upon [2]. While some learning resources already existed in the form of printed scripts and paper versions of tests, the complete course material had to be rewritten and typed into ILIAS. In 2019, the course held ten interactive learning modules, with more than 1500 mathematics test items, 140 of which use STACK.
Figure 1 shows an overview of the course structure as executed at DHBW Mannheim since 2014. The programme runs in the months leading up to a new semester, and starts with a diagnostic self-test covering the entire pre-course's syllabus. See also recommendations by SEFI mathematics working group [6], and cosh [1].
Depending on their diagnostics test results, students may access the different learning modules. Each course provides text, graphs, animations, examples and exercises, and at the end of each module, students can take a subject-related test consisting of 10 to 15 randomised questions. Students who want additional support can enrol in e-tutored courses, where their learning process is structured and monitored by e-tutors. Students can then discuss problems and test results with peers and e-tutors, and are required to upload completed exercise sheets.
During induction week, all participating first year students take a final test at the University’s computer laboratories. Since 2014, more than 2800 students have participated in the diagnostic pre-test and the pre-course at DHBW Mannheim. This corresponds to approximately 560 students per year, which is around 80% of the cohort.
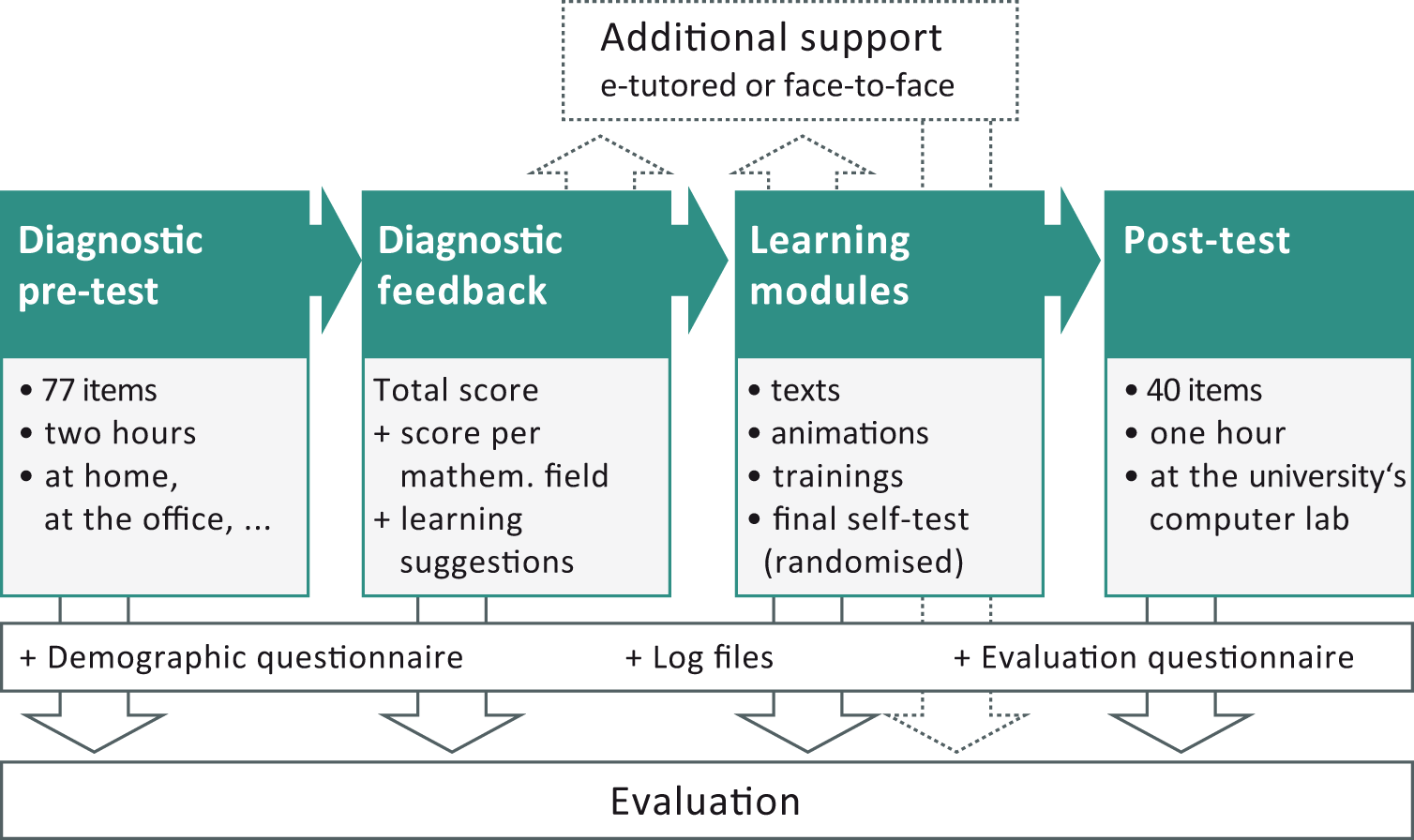
While the diagnostic self-test aims at informing learners of their level of knowledge in relation to the curriculum, the self-tests provided in the ten different courses are designed to encourage learners to independently practice their skills.
Question Construction
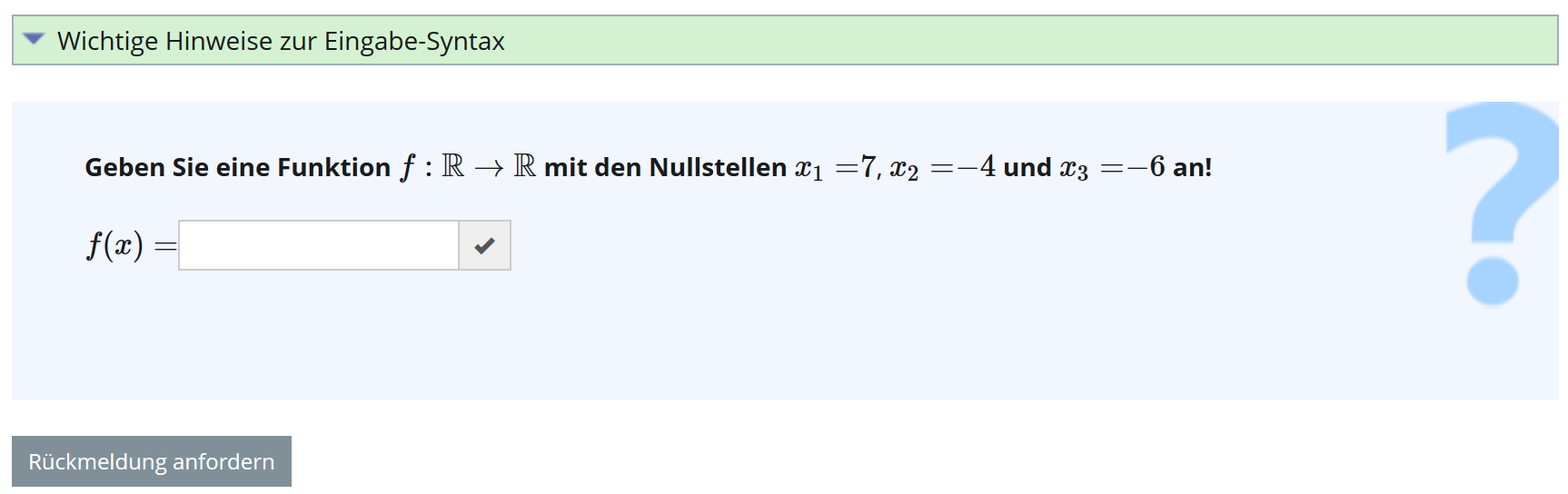
Figure 2 shows an example of an optes question in ILIAS. Students can click the checkmark next to the input box to have their answers validated by the system. On top of the question, the student can click to pop-out an explanation of the input syntax. The question is graded by clicking on “Rückmeldung anfordern”, which means "Request feedback".
In this example, the student is asked to give an example of a function with three given zeroes. There are no other constraints, and in particular the function can also have more zeroes. The given zeroes are randomly generated, so the student can restart the test to try a variant of the problem with different constants.
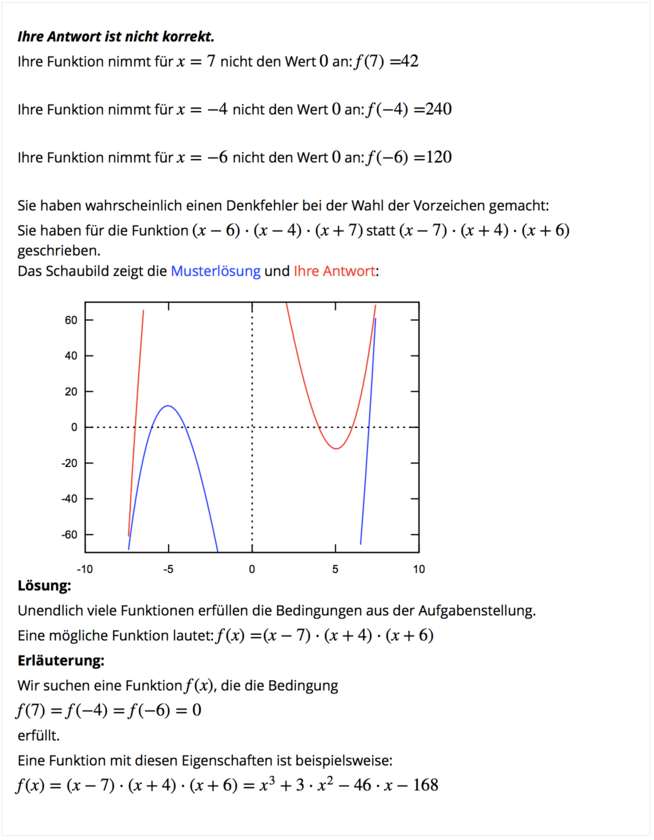
optes questions focus on providing good feedback to students [8]. Feedback incorporates partial marks, if the student for example entered a function with only one or two of the given zeroes, and visuals, by for example graphing the student's answer (in red) against a correct answer (in blue). The student is also shown the value of their function at the three given points and given a model solution. optes questions are great examples of effective use of STACK's feedback features.
Results
The major goal of the optes project was to improve students‘ self-study abilities in mathematics related subjects. Using data collected from the first evaluations phase of the project, the researchers studied the influence of taking the pre-course on different variables. They found that the biggest factor in study success was a student's previous knowledge and secondary school scores. However, they also found that the pre-course could be very effective at improving first-year performance. Of the students whose performance were at risk, those who scored highly in the pre-course also did better in their first year of study. These were the students with poor prior study success or little domain-related knowledge. Self-test engagement was also found to have significance, as they were related to both pre-course gains and first-year performance.
Challenges
A major advantage of learning management systems is their ability to provide automated feedback to students. Instructors are hence relieved from the load of marking hundreds of exercises, and students appreciate the immediate response of the system. However, writing feedback for web-based mathematical problems is time-consuming, and these efforts may grow exponentially when the questions have multiple correct answers. To help soften this burden, it is important to share STACK questions, not only across pre-course projects but also across universities and e-learning platforms.
Enablers
A major enabler for the project was the initiative to integrate STACK into ILIAS. If this crowd funding initiative had failed, optes may have had to choose a less suited CAA system.
Furthermore, a lot of institutional support enabled this project. While all resources developed by optes are Open Educational Resources (OER), the implementation of the learning material at third party universities or educational institutions demanded staff and technical infrastructure to install ILIAS and STACK. Staff and technical support helped administer the pre-course and adapt the learning material to each university’s needs. Furthermore, the e-tutor system was enabled by lecturers and older students who took the time to learn to use STACK so they could help pre-course participants as e-tutors.
What's Next?
Since 2019, the rollout of optes to other universities and institutions has begun, and as more and more lecturers use the optes resources, the STACK community in Germany continues to grow. This community is largely represented by the working group "Mathe digital". Lecturers are encouraged to develop and contribute their own questions, resulting in a growing and improving database of available STACK questions.
The researchers continue to evaluate the data from the project. When this analysis is finished, it will be possible to better identify the strengths and weaknesses of the course structure.
Like all projects funded by the German BMBF programme "Quality pact for teaching", optes will be finished by the end of 2020. The developed concepts and course material, however, will be used and developed further at the optes partner universities and at all universities and institutions that share the material. Future plans include incorporating adaptive testing and expanding the work to other subjects and topics, such as mathematics for business and psychology courses.
References
[1] COSH Cooperation Schule Hochschule. Mindestanforderungskatalog mathematik. 2014.
[2] K. Derr. Identifying consistent variables in a heterogeneous data set. Electronic Journal of e-Learning EJEL, 15(1):82-93, 2017.
[3] K. Derr, R. Hubl, and M. Z. Ahmed. Prior knowledge in mathematics and study success in engineering. informational value of learner data collected from a web-based pre-course. European Journal of Engineering Education, 10(3):1-16, 2018.
[4] C. J. Sangwin and I. Jones. Asymmetry in student achievement on multiple choice and constructed response items in reversible mathematics processes. Educational Studies in Mathematics, 94:205-222, 2017.
[5] B. Alpers. A framework for mathematics curricula in engineering education. 2013.
[6] M. Weigel, K. Derr, R. Hubl, and T. Podgayetskaya. Stack-aufgaben im formativen eassessment: Einsatzmoglichkeiten des feedbacks. Zenodo, 2019.
[7] M. Weigel, K. Derr, R. Hubl, E. Mechelke-Schwede, and T. Podgayetskaya. Inhaltliche und technische aspekte des automatisierten feedback. einsatz des fragetyps stack im formativen eassessment. Beitrage zum Mathematikunterricht 2017, 1185-1192, 2017.