Enhancing proof assessment in STACK through Parson's problems

Salvatore Mercuri

Introduction

Proof is the cornerstone of mathematics and as students advance through an undergraduate degree, proof becomes the principal mode through which they learn and practise mathematics. In this case study we will describe recent developments in STACK that enable new ways of automating the assessment of proof. These features not only allow us to move more content of an undergraduate mathematics degree onto STACK, but they also present opportunities for students to interact with and understand proof in new and interesting ways.

A typical mathematical proof might look something like the following.

Theorem. An integer $n$ is odd if and only if $n^2$ is odd.
Proof. If $n$ is odd then, for some $m \in \mathbb{Z}$, we can write $n^2 = (2m + 1)^2 = 2(2m^2 + 2m) + 1$, which is odd. On the other hand, if $n$ is even then, for some $m\in\mathbb{Z}$, we can write $n ^ 2 = (2m)^2 = 2(2m^2)$, which is even. $\square$

Free-flowing text-based arguments like the above are the norm in mathematics education and research. However underlying each proof is a formal logical structure. For example, the above proof can be written in a more structured way.

Theorem. An integer $n$ is odd if and only if $n^2$ is odd.
Proof.
($\Rightarrow$) If $n$ is odd then $n^2$ is odd.

Assume that \(n\) is odd.

Then we can write \(n = 2m + 1\) for some \(m \in \mathbb{Z}\).

Therefore \(n^2 = (2m + 1)^2 = 2(2m^2 + 2m) + 1\), which is odd.

(\(\Leftarrow\)) If \(n^2\) is odd then \(n\) is odd.

We reformulate "If \(n^2\) is odd then \(n\) is odd" as the contrapositive.

If \(n\) is not odd then it is even, so \(n = 2m\) for some \(m \in \mathbb{Z}\).

Then \(n^2 = (2m)^2 = 2(2m^2)\) is even, and therefore not odd.

Structured proof writing can be helpful in clarifying the logic of a proof. It can allow us to signal concepts such as scope of variables; for example, the $m$ that appears in the $(\Rightarrow)$ block is different to the $m$ that appears in the $(\Leftarrow)$ block. Variable scope is a core part of any programming language where it is typically signalled through the use of structural elements, usually a mix of indentation and/or braces. Anyone familiar with programming may already have noticed that the above structured presentation of a mathematical proof resembles code to some degree.

In computer science, Parson's problems were introduced in 2006 [3] and have since been a popular method for automating the assessment of programming ability. These problems involve dragging and dropping lines of pre-written code into the correct order and structure so as to provide a functioning program which performs the requested task. Parson's problems have been shown to be highly effective for early-stage students in programming because they reduce the cognitive load required to remember correct syntax and generate steps [4]. Thinking about proof as a formally structured logical argument, as in the second example above, can help us to apply Parson's problems to proof.

In the next two sections, we will describe more details of the representation of mathematical proof as formal structures and assessment algorithms that can be leveraged to deliver automatic line-by-line feedback. After that, we will talk about how Parson's problems were implemented in STACK before finishing with a look ahead to future possibilities in automating proof assessment.

Mathematical proof as trees

A suitable representation of mathematical proof that can allow us to understand when an ordering of pre-written proof steps is considered a correct proof. Sometimes, a given proof consists of a set of statements that can only be given in a single correct order. Consider the following example:

Theorem. If an integer $n$ is odd then $n^2$ is odd.
Proof.

1. Assume that $n$ is odd.
2. Then we can write $n = 2m + 1$ for some $m \in \mathbb{Z}$.
3. Therefore $n^2 = (2m + 1)^2 = 2(2m^2 + 2m) + 1$, which is odd.

As written, the above proof can only ever appear in that order, because step 2 depends on the assumption in step 1, and the calculation in 3 makes use of the variable $m$ which is introduced in step 2. However, this is often not the case. In fact, because the order of the ($\Rightarrow$) and ($\Leftarrow$) blocks does not matter, the following is an alternatively ordered correct proof of the example in the previous section.

Theorem. An integer $n$ is odd if and only if $n^2$ is odd.
Proof.

(\(\Leftarrow\)) If \(n^2\) is odd then \(n\) is odd.

We reformulate "If \(n^2\) is odd then \(n\) is odd" as the contrapositive.

If \(n\) is not odd then it is even, so \(n = 2m\) for some \(m \in \mathbb{Z}\).

Then \(n^2 = (2m)^2 = 2(2m^2)\) is even, and therefore not odd.

(\(\Rightarrow\)) If \(n\) is odd then \(n^2\) is odd.

Assume that \(n\) is odd.

Then we can write \(n = 2m + 1\) for some \(m \in \mathbb{Z}\).

Therefore \(n^2 = (2m + 1)^2 = 2(2m^2 + 2m) + 1\), which is odd.

Our representation of proof should capture such non-unique orderings of a proof. This begins by recognising that a proof may contain a number of structural logical arguments, which may decompose a proof into a number of sub-proofs whose orderings usually do not matter. For example, an "if and only if" proof decomposes into two sub-proofs, one for the "if" direction and another for the "only if" direction, as in the above example. The most common forms of structural logical reasoning in mathematics fall under one of the following:

• If and only if: decomposing the argument into two commutative sub-proofs.
• Proof by induction: decomposing the argument into the base case and the inductive step.
• Exhaustive cases: decomposing the argument into a number of commutative cases.
• Contradiction or the contrapositive: which reformulates an argument and does not involve any decomposition.

This decomposition of proofs into sub-proofs allows us to think of proofs as trees, where nodes consist of proof steps and branches consist of direct logical deduction. If the logical deduction involves decomposition into sub-proofs then this branching will be multiple, else it is singular. For example, the above if-and-only-if proof looks like the following.

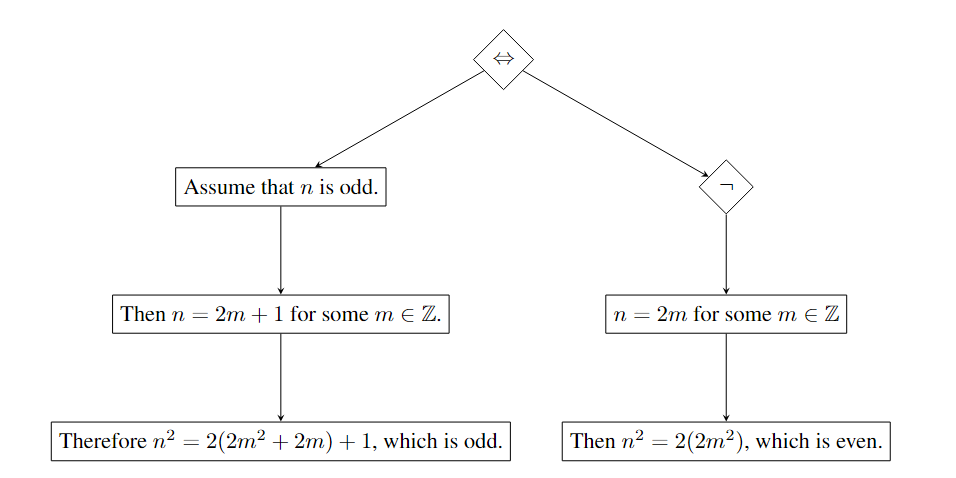
In the above diagram, we represent structural logical reasoning by diamonds and singular deductive proof steps by rectangles. Each structural diamond has its own specific properties; the $\Leftrightarrow$ diamond, for example, has the property that it is a binary node whose children commute.

To implement proof trees in STACK, we developed a Maxima proof library in STACK called prooflib.mac which contains a number of functions which represent various structural diamond nodes. For example, the function proof_iff takes two arguments and satisfies proof_iff(A, B) = proof_iff(B, A), whereas the function proof takes an arbitrary number of arguments which must appear in order. See the documentation for more information on these proof functions.

A proof assessment algorithm

A Parson's problem involves dragging and dropping pre-written lines into order, so that the student's answer is a list. However, the teacher's model answer for a Parson's problem in STACK takes the form of a proof tree. This is so that the system is able to capture all the non-unique correct proofs for the given set of proof steps. To understand whether the student's flat list of steps is a correct ordering we first use the proof-tree representation to generate all possible correct orderings of the steps as a list. Then, we iterate over all correct list and compare the student's list using the Damerau-Levenshtein distance, which we will describe in more detail below. If, for some correct list, this metric returns zero then the student's answer is a match and they have a correct proof. If not, then the student has an incorrect ordering of steps and, moreover, the Damerau-Levenshtein distance allows us to track exactly which modifications the student needs to make to change their incorrect proof into a correct proof. This algorithm enables us to not only assess correctness, but also automatically generate line-by-line feedback on the student's answer.

The Damerau-Levenshtein distance ([1], [2]) is used to measure the minimum number of edits needed to go from one string to another. Here, the permissible edits include:

• insertion: "ick" --> "tick";
• deletion: "tick" --> "ick";
• substitution: "sick" --> "tick";
• transposition: "angel" --> "angle".

This can easily be applied to any arbitrary sequence, rather than strings. In particular, we can look at two lists of proof steps and apply the Damerau-Levenshtein algorithm between them to compute the specific insertions, deletions, substitutions and transpositions of proof steps required to go from one to the other. The diagram below shows the overall assessment algorithm used within a Parson's question in STACK.

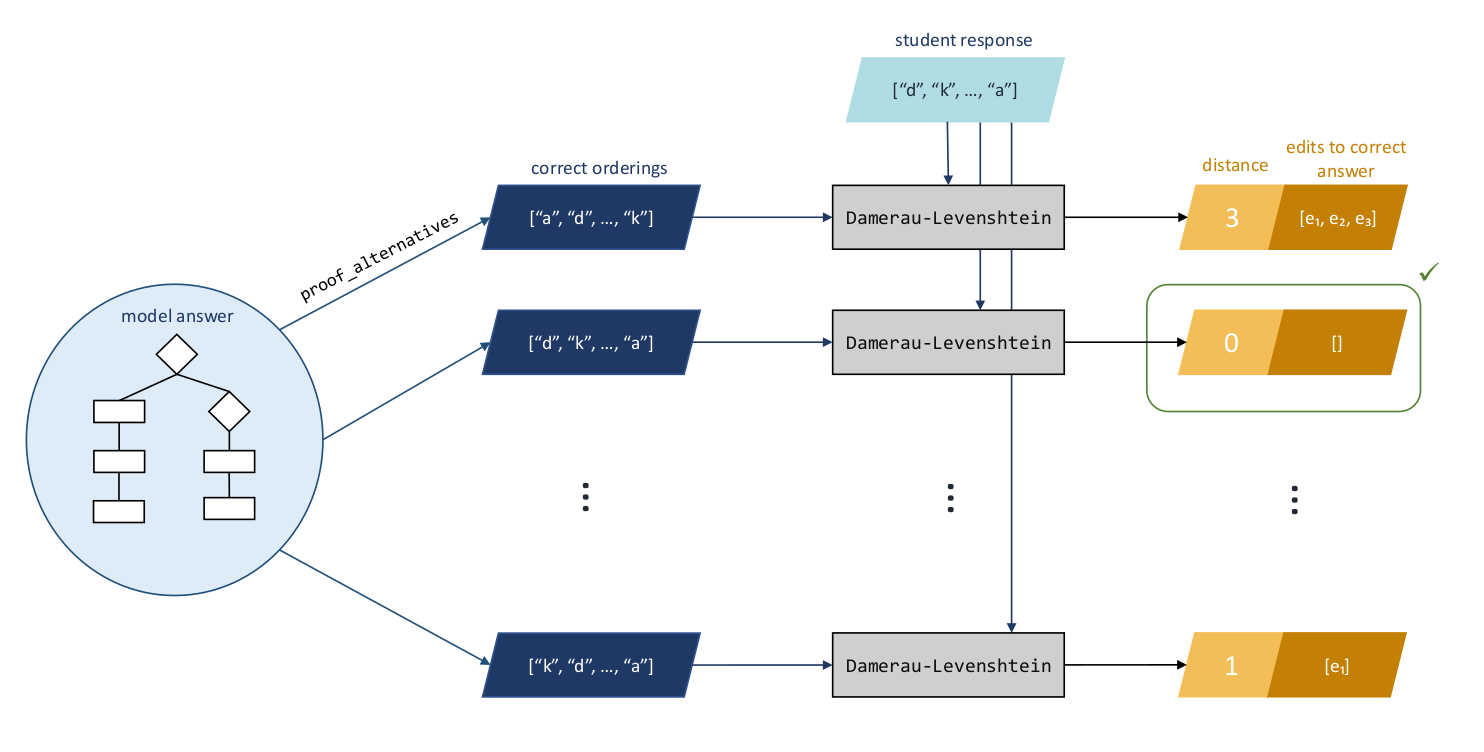
Within the Maxima proof library prooflib.mac provided in STACK, there are functions that allow users to compute each link in the above diagram. The function proof_alternatives will take an author's model answer proof tree and compute all possible alternatives. The function proof_assessment will compute the smallest Damerau-Levenshtein distance between a student's input and all the correct alternatives, and for that minimum pair it will give the edits required to get from the student's answer to a correct answer (the green box in the above diagram). Finally, proof_assessment_display will generate a visual representation of the edits the student needs to make to correct their answer. Some examples of how this looks on the question page in STACK for non-unique correct answers and an incorrect answer with automatic line-by-line feedback are given in the following figures.

Writing Parson's problems in STACK

To write a Parson's problem in STACK, the library prooflib.mac should be loaded using stack_include_contrib within Question variables. This makes available all the various proof functions needed to construct proof trees and assess answers. All of the pre-written steps and the model proof-tree answer can be written in the Question variables field, see the documentation for details on the syntax required. The main drag-and-drop functionality is achieved through the use of the Sortable JavaScript library, which is a widely used and supported library for drag-and-drop features. In STACK, this functionality is wrapped by a parsons block so there is no need for the author to write any JavaScript themselves. However, authors are able to customise the drag-and-drop functionality to a certain degree, either by block header parameters in the parsons block or through the options field in the block contents. For further details on how to get started writing a Parson's problem, follow the documentation.

The future of proof assessment in STACK

As we have seen, writing proofs in highly structured ways can help us capture important properties of proof and enable the application of Parson's problems to this area. However, structured proofs have other benefits such as clarity of logic and scope which can be helpful to early-stage learners. A future priority for proof assessment in STACK will be developing ways that enable students to interact with proof in such structured ways. This could be through allowing indented blocks within the current style of Parson's problems, for example, allowing the student's answer to also represent a tree rather than just a flat list.

Within recent years, there has been a rise in research in formal programming languages such as Lean. Mathematical proofs written in Lean, for example, can be automatically verified as correct or incorrect. This growing research has even led to recent successful applications of Lean in artificial intelligence at the International Mathematical Olympiad in 2024. While it seems natural to harness the power of languages such as Lean for automating proof assessment in STACK, these languages do not form a standard part of a mathematics curriculum nor have they been shown to increase a student's level of understanding of a proof. So we cannot currently assume students or question writers are able to directly interact with such formal programming languages. It may be the case that future research within AI and automated theorem proving may help to bridge the gap between formal programming languages and mathematical education, unlocking a raft of benefits for automated proof assessment.

References

[1] F. J. Damerau, "A technique for computer detection and correction of spelling errors", Communications of the ACM, 7 (3): 171-176 (1964)

[2] Vladimir I. Levenshtein, "Binary codes capable of correcting deletions, insertions, and reversals", Soviet Physics Doklady, 10 (8): 707-710, (1966)

[3] D. Parsons and P. Haden, "Parson’s Programming Puzzles: A Fun and Effective Learning Tool for First Programming Courses", Proceedings of the 8th Australasian Conference on Computing Education, 52: 157-163, (2006)

[4] D. Paul, A. Luxton-Reilly, and B. Simons, "Evaluating a new exam question: Parson's problems", Proceedings of the Fourth International Workshop on Computing Education Research", ICER: 113-124, (2008)

Partners

This work is part of the Knowledge Transfer Partnership between the University of Edinburgh and IDEMS International, funded by Innovate UK.