Adaptive Self-learning Exercises

Ruhr-Universität Bochum

Michael Kallweit

Abstract

At the Ruhr-Universität Bochum, students from all disciplines are offered digital mathematics tasks in an e-learning course for self-study in order to prepare and revise. These questions make intensive use of the randomisation and differentiated feedback options of the STACK question type. Some tasks have been supplemented by adaptive exercises, which guide the students through complex tasks. These adaptive tasks have had great success, are shown to have the same level of student engagement as paper-based tasks and be a better predictor of exam performance.

Introduction

At the Ruhr University Bochum, digital exercises have been used in courses at the Faculty of Mathematics since 2011, and since 2013 this has included STACK. In 2015, a cross-curricular e-learning course was set up, in which students can repeat and process selected topics for exam preparation by themselves. The course takes advantages of Moodle's gamification features: students gain points for engaging with quizzes, contributing to a "level". They also earn badges for completing material in a short time or with a high mark. Additionally, students have access to digital tutorial support.

In addition to these features, the University wanted to add learning exercises that adapt to students' needs.

Motivation

In online assessment, weekly digital exercises are often done in "examination mode", that is, where students complete tasks in a given timeframe without interacting with the teachers in the meantime. Normally students are only allowed one attempt at the question, and differentiated feedback is only available for the students after the deadline. However, experience shows that students rarely use the detailed written feedback provided and are satisfied with just seeing their score. This observation is consistent with the students' responses to manually graded paper-based homework.

Additionally, often valuable reflective loops that promote learning are omitted. As highlighted by Hattie's meta-analysis [2 and 3], it is important to increase students' interactivity with the feedback on their solutions. According to [4], good feedback should show concrete possibilities of how gaps in skills can be closed by students.

Contrast this with tutorial lessons, where teachers often help students find a solution path. In the form of minimal assistance, teachers will intervene to help students achieve steady progress in dealing with a problem. If the students take an erroneous path to a solution, the teacher not just corrects the error, but will instead take the student on the path through the task. After being steered on the right path, the student will often fix the error by themselves. This procedure is known as instructional scaffolding: with just minimal support from the teacher, the students can master the individual tasks themselves, and can actively reflect on difficulties and mistakes during the process to close gaps in their knowledge.

The developers at Ruhr-Universität Bochum wanted to bring this concept to online assessment: to build an online assessment system that can carry out instructional scaffolding to help students find a solution path. STACK was ideal for this, as its features in providing specific feedback depending on the properties of students answers provide a great foundation for an adaptive system.

Adaptive self-learning approach

Instead of being confronted by a teacher in a tutorial group, students can process adaptive digital self-learning tasks. Following the above principles, students follow an adaptive path of intermediate step tasks in small steps after submitting an incorrectly answered task. The intermediate steps focus on concrete knowledge and skills that must be combined to solve the original task.

The adaptive methods were tested in entrance exams at secondary level II schools, through diagnostic error analysis tools [5,6,7]. The goal of this was to isolate the underlying errors behind why students incorrectly process digital tasks. Using digital tasks with STACK and a complex composition of digital tasks, the researchers achieved a considerable error detection rate of about 90%.

Development of adaptive self-learning tasks

Adaptive self-learning tasks follow the scaffolding principle. The error analysis and subsequent presentation of intermediate steps take place within the potential response trees of a STACK question, and offer added value compared to traditional digital tasks:

• In contrast to tasks in "examination mode", students actively deal with difficulties and errors. These are independently overcome by support in small steps and aim at a lasting learning success and increased motivation.
• Even with randomized STACK tasks, intermediate exercises refer to the task set at the beginning. A reference to the initial problem remains visible along the entire learning path.
• There are no limits on the design and variety of adaptive paths through the task. With each intermediate step, the next step can be selected on the basis of the student's individual input.
• The individual paths through the task are included in the source code of the individual STACK task, which allows questions to be easily shared between courses.
• The STACK Response Analysis Tool gives teachers insight into the paths taken by students.

Technical implementation

Moodle currently only offers limited possibilities for adaptively designing a sequence of tasks in tests. Hence, the adaptive tasks were introduced at the level of individual STACK questions. For each question, the potential response tree analyses the student's solution, and if they have made an error, shows a link to the starting point of an individual path. By including an externally stored Javascript file, the next intermediate step exercise becomes visible only by clicking on a button. The analysis of the input for this intermediate step is also stored in a response tree which adaptively defines the subsequent tasks. By repeating steps and integrating additional ones, the adaptive procedure can simulate real tutorial support.

Example

The following elementary example for matrix multiplication illustrates the central principles of the adaptive task format:

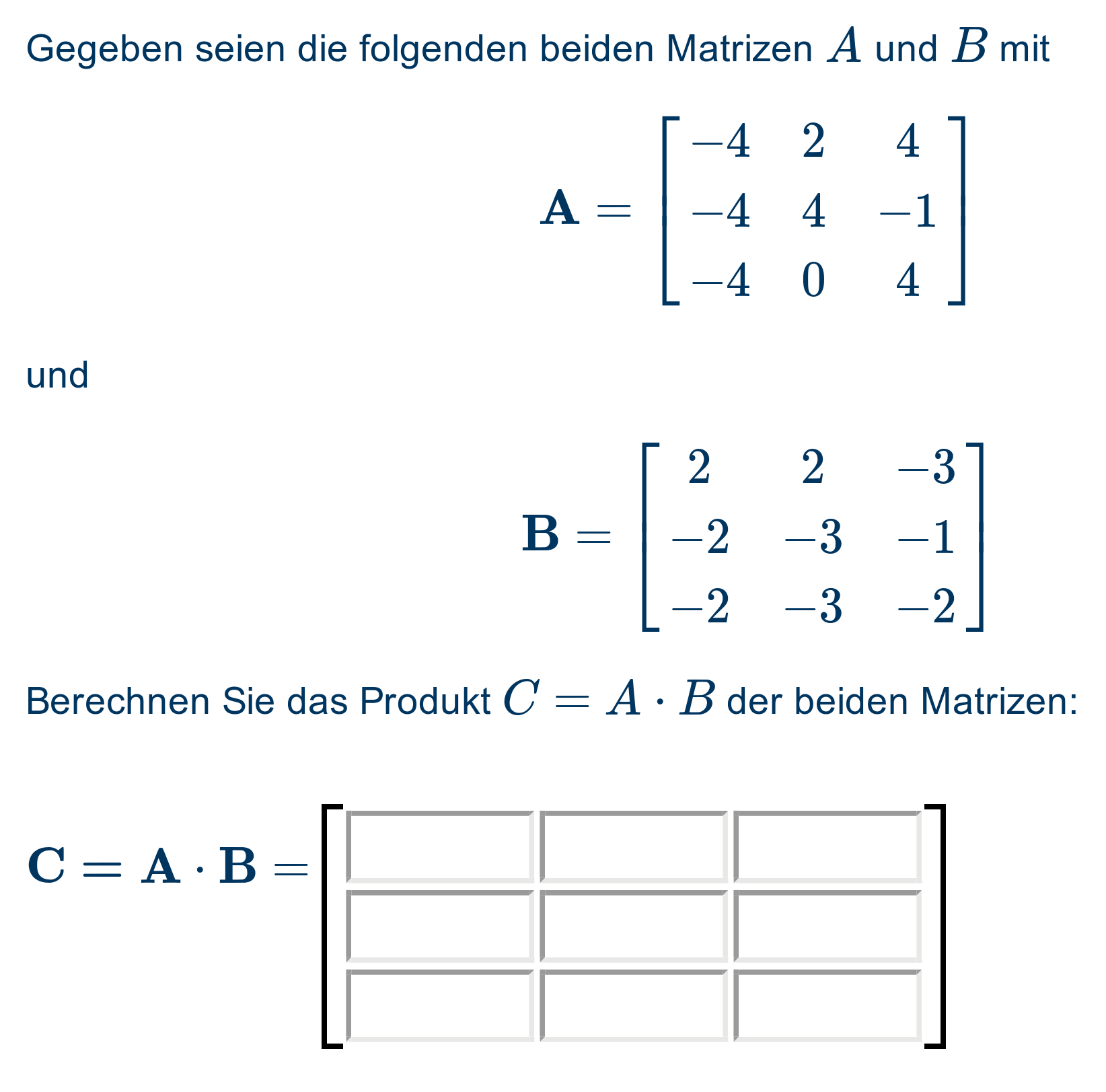
If the input of the solution is incorrect, the student is informed that they can work on the task again in guided intermediate steps via the "Weiter" ("Next") button.

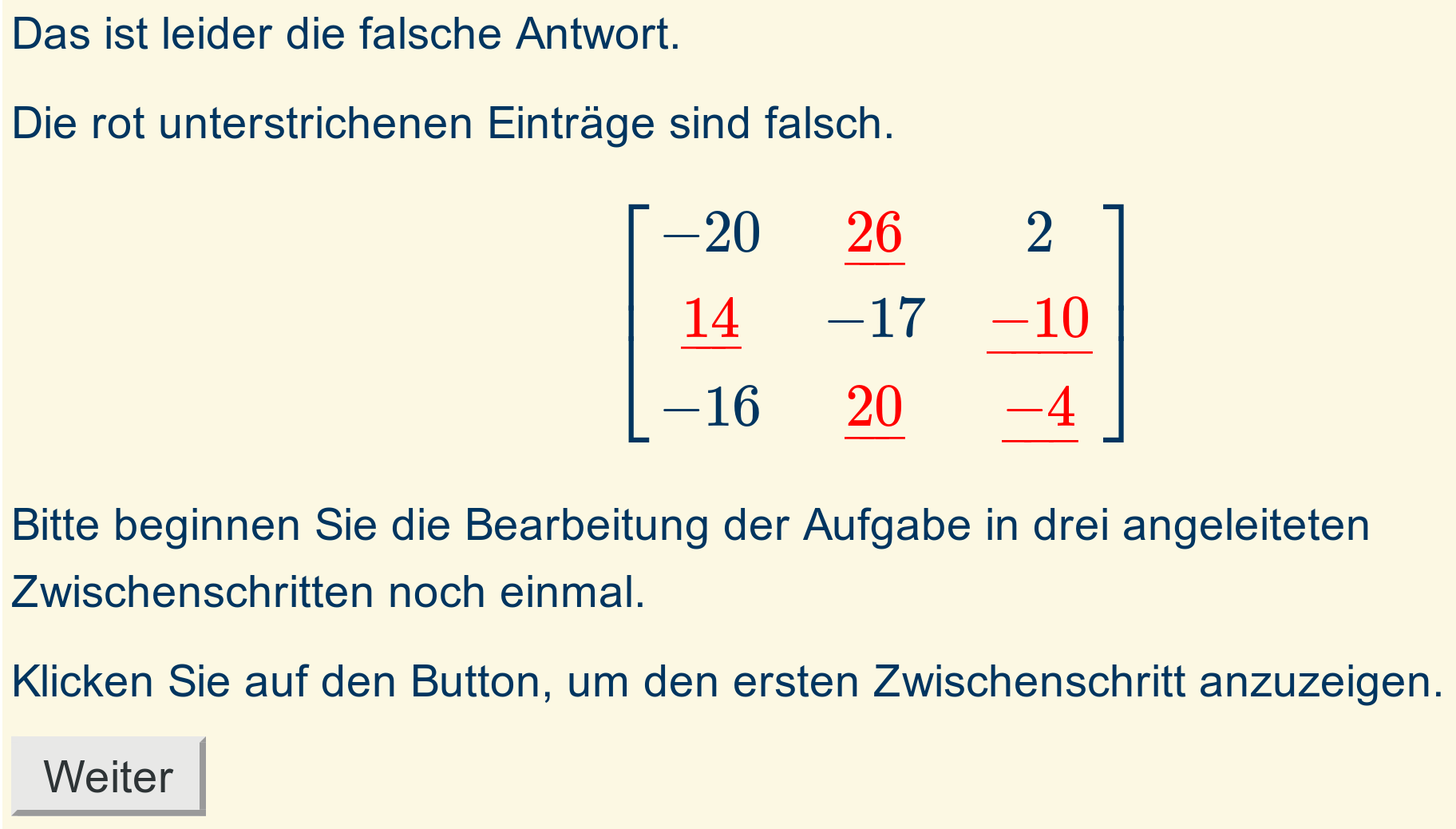
The first intermediate step then opens directly below the actual task, in this case asking students to identify the rule that is used when calculating matrix products. Subsequent steps will be available each time a step is correctly completed and the student clicks "Next"

The entire adaptive path with all intermediate step tasks has the following structure.

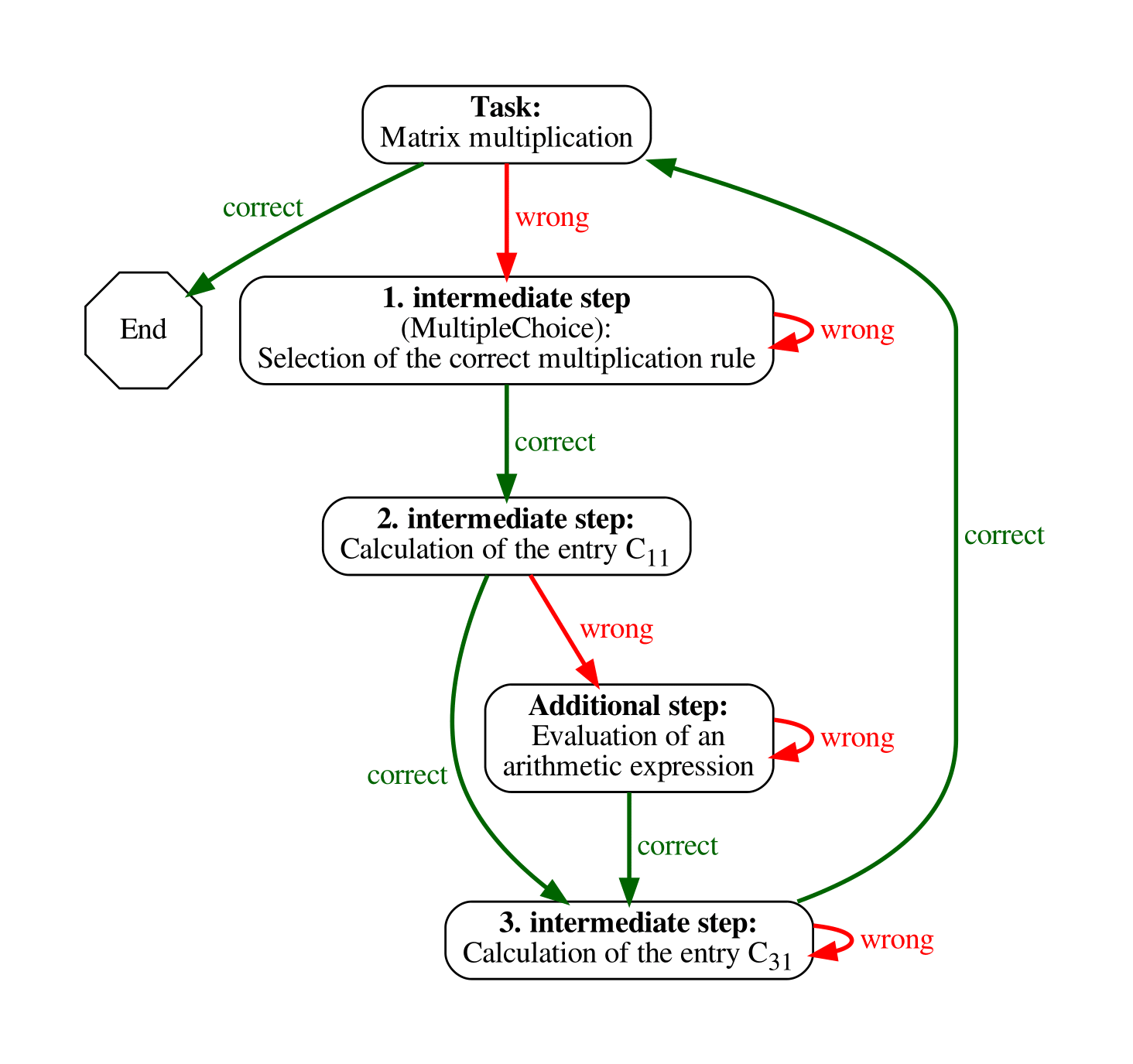
It is also possible to ask students to make a decision about which direction they want to take.

Branches at which students make decisions about which direction they want to take are also possible. Overall, the feedback can be structured in a variety of ways according to Zech's hierarchy levels, with a focus on motivation, strategy or content help [8].

Results

When comparing the University's new online assessment to their old, multiple-choice based system, several improvements become apparent. In multiple choice questions, you can only have a finite number of "distractors", but in STACK you can give feedback on an unlimited number of answers. In particular, the developers compared a question about expanding (2x+3y)^2, and found that while the old system had only 9 distractor options, the STACK system had registered 41 different answers over its lifetime, which could be grouped into 28 different types of mistakes. This is a major improvement on the number of mistakes students can receive specific feedback about.

Additionally, the developers wanted to compare the performance of paper-based and digital homework. Across all courses, they did not find any significant difference in how many tasks students complete between the two systems. This is encouraging; the University saves resources by not relying on human markers for homework, and this confirms that they have not lost any functionality or student engagement by moving towards online assessment. For the course "Mathematics for Chemistry", the correlation between paper-based homework scores and exam scores was found to be 0.56, but the correlation between online homework scores and exam scores was 0.63. Similar results were found for the other courses at the University. Hence, online quiz scores are a better predictor for exam scores.

Challenges

One of the main challenges of STACK integration was keeping up with new versions. It was important to convince administrators that going through the trouble of updating STACK was worth it, as new updates and features could be important to question authors.

Additionally, there was a challenge in distributing the questions to new users, since Moodle's options for managing and distributing questions were found lacking. To solve this, a database for managing STACK questions in moodleXML files was created, which included more sophisticated search options. For each question, the system generates an overview pdf file with a short description, information on available languages, screenshots and an automatically generated overview of the potential response trees. About 700 questions are in the database, and because of its usability, it is easy to convince new users that it is simple to find good STACK questions.

Enablers

It was helpful to have a strong community of STACK users to help with projects. For example, one of the lecturers held a seminar to teach effective STACK usage to students training to become school teachers. The students of this class became a valuable community of STACK users willing to help with other projects. Additionally, it was valuable that STACK had been translated to German, as this allowed the University to easily spread STACK to other German institutions and build good partners.

What's Next?

The STACK courses at Ruhr-Universität Bochum continue to be improved on. Future additions may include using more sophisticated features in questions, such as equivalence reasoning inputs and interactive JSXGraph visuals.

References

[1] M. Kallweit and E. Glasmachers. Adaptive selbstlernaufgaben mit STACK. 2019.

[2] J. Hattie. Visible learning: A synthesis of over 800 meta analyses relating to achievement. Routledge, 2009.

[3] J. Hattie and H. Timperley. The power of feedback. Review of Educational Research, 77(1):91-112, 2007.

[4] D.J. Nicol and D. Macfarlane-Dick. Formative assessment and self-regulated learning: a model and seven principles of good feedback practice. Studies in Higher Education, 31(2):199-218, 2006.

[5] R. Bruder, N. Feldt Caesar, A. Pallack, G. Pinkernell, and A. Wynands. Mathematisches grundwissen und grundkonnen in der sekundarstufe ii. W. Blum et al. (Hrsg.), Bildungsstandards aktuell: Mathematik in der Sekundarstufe II, pages 108-124, 2015.

[6] M. Schaub. Einsatz des elementarisierenden testens im ein- und ausgangstest des online vorkurses vemint. Beiträge zum Mathematikunterricht 2018., pages 1567-1570, 2018.

[7] F. Zech. Grundkurs Mathematikdidaktik. Theoretische und praktische Anleitungen für das Lehren und Lernen von Mathematik. 1978.