Developing a Fully Online Course

The University of Edinburgh, UK
Interview with George Kinnear and Richard Gratwick
Abstract
STACK is used in the completely online course "Fundamentals of Algebra and Calculus". The course is designed to prepare students for Higher Education (HE) study at the University of Edinburgh, where incoming students have a wide range of mathematical backgrounds. The main barriers were the risk of students using online answer engines to answer questions, and the lack of community. The organizers attempted to address this by clever question design and creating "autonomous learning groups". The course was enabled by University support, both in the form of a dedicated learning-technologist post and assistance from colleagues. Subsequent diagnostics test results indicate this course was successful.
Introduction
Approximately six hundred students typically study first-year mathematics courses at the University of Edinburgh. They have a wide range of mathematical backgrounds and attainments. "Fundamentals of Algebra and Calculus" (FAC) was introduced as an additional course, approximately covering SQA Advanced Higher Mathematics and A-Level Further Mathematics, to address the needs of this diverse group. Since some incoming students do not have the chance to take these higher qualifications before coming to university, the course fulfils a role as part of the University’s Widening Participation strategy, enabling access to mathematics courses for a wider range of students, e.g. students admitted through contextual admissions. This also was an attempt to address a concern from the University that one reason for undergraduate non-continuation was a lack of preparation for the mathematical components of students’ degree programmes, particularly those students on non-mathematics degrees within the College of Science and Engineering. Increasingly, the second-semester year 1 "Calculus and its Applications" course had been adapted to address these problems. However, staff and students felt that it recently contained too much material. FAC aimed to relieve some of the pressure on this course.
FAC was delivered as a completely online course to make it scalable, since the above issues are not unique to the School or the University. FAC plays a role in addressing the so-called “mathematics gap” of attainment, preparing students from a wide range of mathematical backgrounds for HE study, and as such could easily see demand both across the University and beyond.
Why Use STACK?
FAC is essentially a course in mathematical techniques, assessing routine computation. STACK precisely lets teachers assess such questions automatically and give tailored feedback to students. Quite sophisticated questions can be implemented, for example “give an example” type questions, asking students to provide examples of e.g. a quadratic with given roots, or a sequence with certain monotonicity or boundedness properties. These are important for "retrieval practice", that is, encouraging students to recall previous topics.
Execution
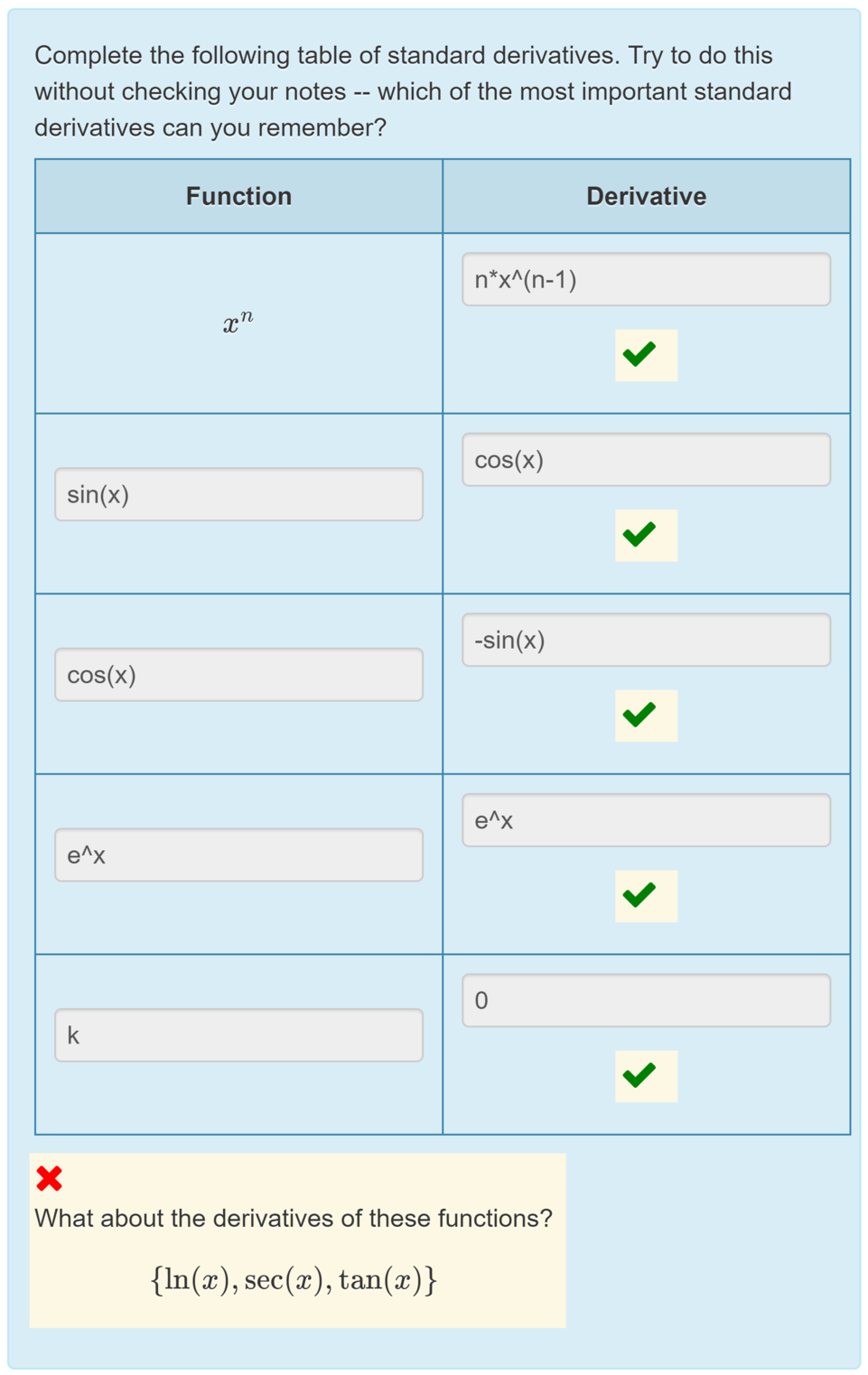
The course is worth 10 ECTS credits, and consists of approximately 200 hours of work for the student. The course is delivered in ten weekly units, each comprising a number of quizzes intended for students to work through during that week. Each week ends with a 90-minute "Practice Quiz" the student can take an unlimited number of times, and a 90-minute "Final Test" only allowing one attempt. The test is either given a grade of fail (0-80%), mastery (80-95%) or distinction (95%-100%). The high pass mark encourages students to master a topic before moving on. The final grade is determined by combining the results of the 10 "Final Tests" (worth 80%) with a final 2-hour test covering the whole course (worth 20%).
The development involved a substantial up-front time investment: writing the material in these quizzes, including over 900 STACK questions. Although some existing questions were borrowed from other courses, the majority of these questions were authored from scratch. The quizzes interleave textbook-style exposition with videos of worked examples, interactive applets and practice questions, and as a result, the questions have a polished and varied look. Two lecturers were involved, each responsible for five units, with final cross-checking and occasional extra contributions.
Research
The design of the course was heavily influenced by educational research. Firstly, the course uses "faded worked examples", that is, presenting a sequence of problems with different amounts of the solution already worked out. For example, a topic might begin with a full worked solution of a problem, followed by a worked solution with the final step as a STACK input, followed by a worked solution with the last two steps as STACK input, and so on. There is evidence that this is helpful for students [2].
Additionally, given the literature on the importance of "retrieval practice" [3], FAC gives plenty of chances for students to recall what they have learned, for example by having quizzes draw on skills from previous weeks. Weeks alternate between algebra and calculus, spacing out practice of the two topics.
Furthermore, the lecturers decided not to make feedback for the final tests available to students until after the deadline, since there is evidence suggesting delaying feedback is helpful for learning [5].
Finally, FAC gives students a chance to create strong "example spaces" [4], that is, sets of examples that a student can recall for a given topic. Example spaces are developed through "give-an-example" style questions, which are easy to write in STACK.
Visuals
FAC uses a lot of graphs and interactive applets to make questions visually appealing. Visual intuition is an important part of learning about functions, so it is appropriate for graphical components to play a significant part in this course. FAC uses both JSX graphs (which can be coded directly in STACK) and external plugins, like GeoGebra. The advantage of JSX graphs is that they are self-contained; there is no need to worry about changes to external programs, or licensing rights. There is, however, a large cost-benefit analysis to consider. JSX graphs are time-consuming and have a steep learning curve, while external applets are often quick to set up and have simple drag-and-drop features.
Results
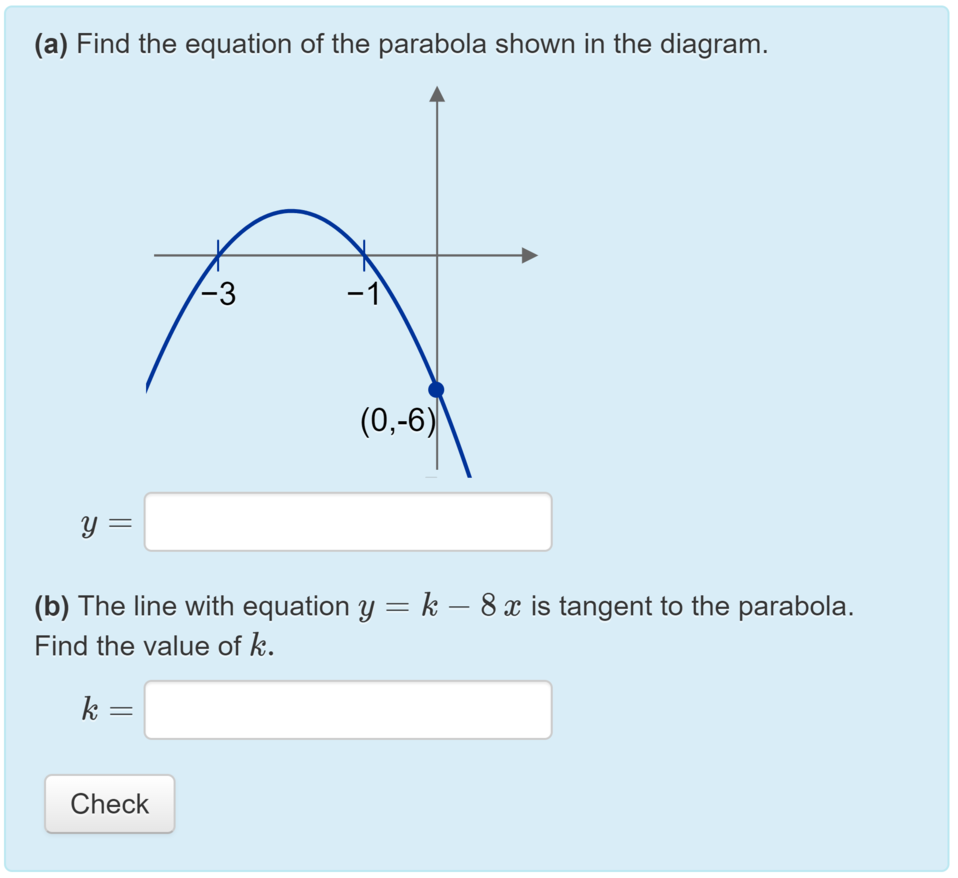
The six hundred students taking the first-semester year 1 "Introduction to Linear Algebra" course sat a diagnostic test (also delivered through STACK) in September 2018. In January 2019, the students sat the test again with the same questions but different random variants. In the September test, students also enrolled on FAC scored on average fifteen percentage points lower than their peers. This is not surprising; FAC will have been recommended to students who felt like they needed more practice in mathematics fundamentals. However, in January after studying FAC, they had gained these fifteen percentage points and were scoring in line with their peers. This is quantitative evidence that FAC has done exactly what was hoped: removed the discrepancy in attainment between the two groups of students.
The lecturers also wanted to know if taking FAC had improved student performance in other maths courses such as "Introduction to Linear Algebra" (ILA) and "Calculus and its Applications" (CAP). Of students scoring similarly in the September diagnostics test, students who took FAC were scoring better than their peers in online quizzes for CAP. They also scored at a similar level to students who did not take FAC in the exams for ILA and CAP.
Challenges
While it is true that authoring a simple STACK question is ultimately straightforward, there was nonetheless a technological hurdle to be cleared. One lecturer was entirely new not only to STACK, but to Maxima and any form of online assessment, and therefore was confronted with quite an intimidating prospect. However, they ended up authoring hundreds of questions without trouble, and are now confident in undertaking significantly more demanding questions. This hurdle was easier to overcome given STACK requires no programming expertise.
The lecturers were mindful of the possibility that students could be working through assessed quizzes in one browser tab, with a tool like WolframAlpha open in another. While ultimately this does no benefit to the student, and it remains their responsibility to ensure submitted answers are their own work, the potential of this kind of abuse should be minimised. This just required a bit of cunning at the level of question-setting: turning “find the derivative of this given function at this given point” into “at what point is the value of the derivative of this given function this given number?”
The limitations of an online course include the difficulties of forming meaningful staff-student and student-student interaction. The lack of real staff-student interaction made it hard to gauge whether the level and volume of material was suitable – anecdotal feedback indicates this was misjudged in at least one of the weekly units. Student-student interaction is important to foster a sense of community. This was addressed by setting up “autonomous learning groups” in which the students could study, in person, once a week, without staff input. Furthermore, students could ask questions in the online forum Piazza, and get in-person help in the MathsBase study room if needed.
Enablers
The University had created a dedicated learning-technologist post to help design the online assessment and write STACK questions. Their work was invaluable for authoring some of the questions, often given only a one-line sketch of the desired question.
The capacity in STACK to clone questions and export questions from other courses was also very useful, making it possible to produce multiple related questions, sharing, for example, a grading structure, without duplicating any work.
Finally, it was an advantage that there is substantial “in-house” support at the University, since STACK is now used across the entire first-year curriculum and increasingly beyond. Hence, there are a number of members of staff with experience of authoring questions, and the students are familiar with it.
What's Next?
A lot of data has been collected in FAC's first year. Quiz responses will be analysed to determine if any questions should be modified. There are also plans to have interviews with students on the effectiveness of the course, which will help identify areas that need work.
The course organiser will be looking at improving the "autonomous learning groups". Since groups were given weekly tasks and asked to upload solutions to a shared Dropbox, the lecturers can see how much students interacted with these groups. Initially, the engagement was very strong, but half-way through the course, a lot of groups seemed to stop meeting. The course organiser will look at ways to improve turnout for these groups.
The course continues to be worked on. The lecturers are considering options for more interactive questions, for example using equivalence reasoning to assess line-by-line arguments, or interactive JSX graphs that ask a student to, for example, "drag a vector so it is perpendicular to another vector".
The success of FAC paves the way for similar methods to be used in different courses. Other schools have shown interest in creating similar online courses, and some students may find it helpful to have an online course teaching even less advanced maths.
References
[1] George Kinnear. Delivering an online course using STACK. In Proceedings of the STACK Conference, 2018.
[2] A. Renkl, R. K. Atkinson, U. H. Maier, and R. Staley. From Example Study to Problem Solving: Smooth Transitions Help Learning. The Journal of Experimental Education, 70(4):293-315, 2002.
[3] H. L. Roediger and A. C. Butler. The critical role of retrieval practice in longterm retention. Trends in Cognitive Sciences, 15(1):20-27, 2011.
[4] P. Goldenberg and J. Mason. Shedding light on and with example spaces. Educational Studies in Mathematics, 65(2):183-194, 2008.
[5] H. G. Mullet, A. C. Butler, B. Verdin, R. Borries, and E. J. Marsh. Delaying feedback promotes transfer of knowledge despite student preferences to receive feedback immediately. Journal of Applied Research in Memory and Cognition, 3(3):222-229, 2014.