Integration using partial fractions and STACK

Meike Akveld, George Ionita, Andreas Steiger

Introduction

The question in figure 1 is a typical exam question for a first year analysis course for civil engineers at the ETH Zürich.

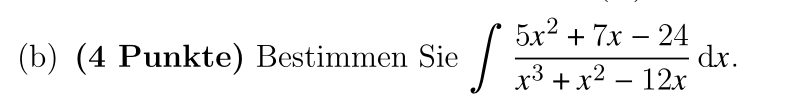
The method needed to solve this question is integration using partial fractions and used to be taught intensively in high school. In most high schools throughout Switzerland this is no longer the case. Of course one could discuss whether it is still necessary, in view of technology, to teach this method, but we do not want to go into this discussion here. We simply assume for the time being that this is still a skill that we want to test in an exam.

In the past we tried two ways of teaching this in a classical lecture. One way was to develop the theory behind it; this was very time consuming and did not really interest most of the students as all they needed in the end was the recipe how to do it. Alternatively we simply gave them the algorithm and did some examples with them in class. This was not satisfying either, as the anti-derivatives that showed up there were not intuitive and maths seemed to have become a tool box (or even black box?) that no one understands, but one just applies, strongly contradicting our beliefs as educators.

In this Case Study we will introduce a more satisfying solution for us to teach this topic, both for students and for lecturers, using STACK.

A Moodle Quiz

We designed a Moodle Quiz which gives a step by step introduction to the method of using partial fractions to integrate rational functions.

The quiz assumes very little prior knowledge. Students only need to know the factor and sum rules for integration and the following anti-derivative

$$\int \frac{1}{x}\, \mathrm{d}x = \ln|x| + c. \quad\quad\quad\quad(1)$$

Students who want to discover this method all by themselves can try to do so, but they will need to invest a fair amount of time (or perhaps refresh their high school knowledge). For others we provide extensive hints and solutions.

Whatever the students decide to do, they will be guided in a natural way to the more complicated anti-derivatives and thereby develop a deeper understanding of the method and the results.

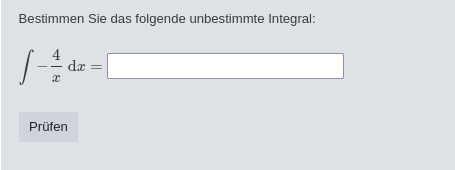
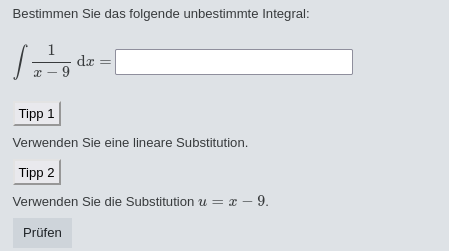
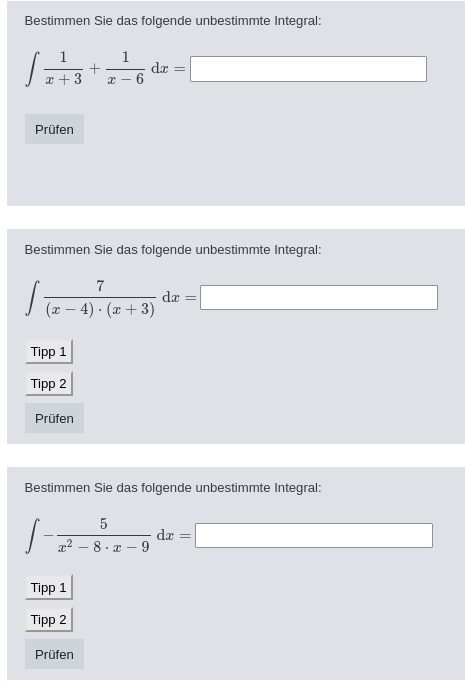
As you can see in figure 2, the quiz is divided into many small sections, each focusing on one step at a time. Figure 3 shows the first section which deals with integrating very simple fractions. All a student needs to know and apply is the basic anti-derivative (1). The question on the left should be straightforward, but for the question on the right a simple substitution is required. If the student does not remember how to do this, the two offered hints should help. We used the setup for hints programmed by Michael Kallweit, see [1]. These hints are not visible upon first opening the question, but can be opened by clicking on a button.

The next series of questions, shown in figure 4, demonstrates the general principle of the quiz. After starting with an easy example the students are led to more general situations. They can always use hints when it is unclear why one question should be seen as a generalisation of a previous one. If the hints do not suffice, the student can also ask for a worked solution and then try the question again. We use gently randomised numbers for new attempts such that some work is required when trying again.

Execution

These STACK questions are part of our so-called Integral Trainer (see [2]). This tool is designed for students to practice and improve their integration skills. The project was conceptualised by two experienced maths lecturers and programmed mainly by our STACK developer.

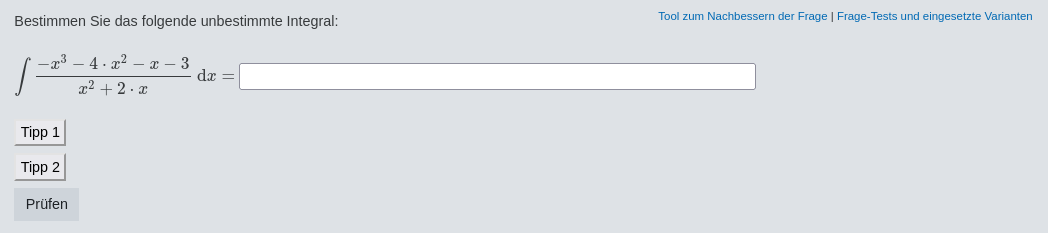
The quiz about rational functions consists of 22 questions and covers rational functions with general quadratic denominator or with cubic denominators with real roots, see figure 5.

None of the questions use the Int answer test, but rather the AlgEquiv answer test. The main reason for this is the constant of integration. Using the latter test the teacher can decide whether or not to give partial credit if only the constant of integration is missing.

Another delicate situation arises when computing integrals of the form $$\displaystyle \int \frac{2x+p}{x^2+px+q}\, \mathrm{d}x,$$ for which the discriminant of the de-nominator is $\Delta = p^2-4q \neq 0,$ see figure 6.

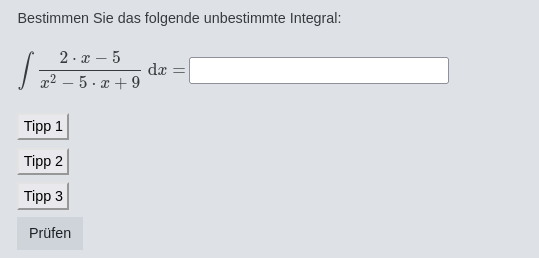
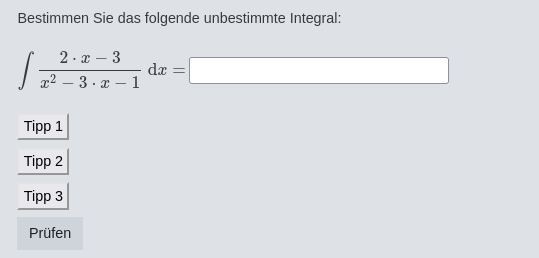
Is the answer $\ln(x^2+px+q)+c$ or $\ln(\left|x^2+px+q\right|)+c$? Of course it depends on the discriminant. If $\Delta < 0$, then both answers should be interpreted as correct, but if $\Delta > 0$, then the absolute value is mandatory. Thus we use a certain trick to distinguish between these situations. The idea is to determine a point that indicates whether the absolute value is needed or not. In this case we considered the $y$-coordinate of the vertex of the parabola associated to the student's answer. Then we calculated its logarithm. If this number has imaginary part equal to zero, then the absolute value is not needed, otherwise it is mandatory.

Unfortunately, the Int answer test did not completely meet our needs. The example above was one of the questions which ignited a technical discussion with Chris Sangwin about the use and limitations of the Int answer test. We hope that this will lead to improvements and calibrations in its design. For more information on how the Int answer test works, we refer to the STACK documentation [3].

Results

This quiz was so far used in two ways: One lecturer instructed the students to solve the first part of the quiz before coming to class (as with a Flipped Classroom) and then only showed some harder examples in class. Another lecturer explained the method in a traditional style and used the quiz as extra practice material. Both sets of data have not been evaluated yet, nor the effect of the quiz on the exam.

What's next?

As a next step we will (certainly) try to evaluate both the data collected in our quiz and the exam results. After we have analysed those, further steps will hopefully become clear.

Reference

[1] M. Kallweit, Programming hints for stack, 2022, last accessed 3 March 2023. [Online]. Available: https://moodle.ruhr-uni-bochum.de/mod/page/view.php?id=1674600

[2] M. Akveld, G. Ionita, and A. Steiger, "Integral trainer," 2022, last accessed 19 April. [Online]. Available: http://www.math.ethz.ch/stack/

[3] C. Sangwin et al., “Stack documentation, answer tests,” 2022, last accessed 19 April 2023. [Online]. Available: https://docs.stack-assessment.org/en/ Authoring/Answer_tests/